Answer:
Test statistic t = 3.12
P-value = 0.001
As the P-value (0.001) is smaller than the significance level (0.05), the effect is significant.
The null hypothesis is rejected.
There is enough evidence to support the claim that the average salary of an employee in the city of Yarmouth is is significantly greater than $55,000 per year.
Explanation:
This is a hypothesis test for the population mean.
The claim is that the average salary of an employee in the city of Yarmouth is is significantly greater than $55,000 per year (Gina's claim).
Then, the null and alternative hypothesis are:
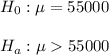
The significance level is 0.05.
The sample has a size n=61.
The sample mean is M=56500.
As the standard deviation of the population is not known, we estimate it with the sample standard deviation, that has a value of s=3750.
The estimated standard error of the mean is computed using the formula:
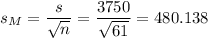
Then, we can calculate the t-statistic as:
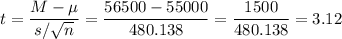
The degrees of freedom for this sample size are:
df=n-1=61-1=60
This test is a right-tailed test, with 60 degrees of freedom and t=3.12, so the P-value for this test is calculated as (using a t-table):
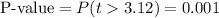
As the P-value (0.001) is smaller than the significance level (0.05), the effect is significant.
The null hypothesis is rejected.
There is enough evidence to support the claim that the average salary of an employee in the city of Yarmouth is is significantly greater than $55,000 per year.