Question

Babies in the United States have a mean birth length of 20.5 inches with a standard deviation of 0.90 inch. The shape of the distribution of birth lengths is approximately Normal. a) Find the birth length at the 2.5th percentile. b) Find the birth length at the 97.5 percentile. c) Find the z-score for the length at the 2.5th percentile. d) Find the z-score for the length at the 97.5th percentile.

Answer 1

a. The birth length at the 2.5th percentile is approximately 18.74 inches.

b. The birth length at the 97.5th percentile is about 22.26 inches.

c. The z-score for the length at the 2.5th percentile is
`\\ z = -1.96`.

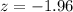d. The z-score for the length at the 97.5th percentile is
`\\ z = 1.96`.

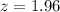Explanation:

We have the following information from the question:

• 
  `\\ \mu = 20.5` inches.
• 
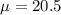  `\\ \sigma = 0.90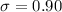` inches.
• Birth lengths is a random variable and follows a normal (or Gaussian) distribution.

Briefly, we can say that:

• A percentile is a value x in the distribution for which a p% of the observations are below it, and (1 - p%) is above it.
• We can use the standard normal table whose values come from the cumulative standard normal distribution to solve this question.

Preliminaries

The standard normal distribution is a normal distribution with
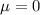`\\ \mu = 0` and standard deviation
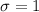`\\ \sigma = 1`. We use this distribution to find any possible probability for normally distributed data.

These values are tabulated in the standard normal table, available on the Internet or in Statistics books.

We also need to standardize raw values (x) into z-scores (or standardized values) using the formula:

`\\ z = (x - \mu)/(\sigma)` [1]

These z-scores represent the distance from the mean,
`\\ \mu`, in standard deviation units. They could be negative, when the standardized value is below the mean, or positive, in which case the standardized value is above the mean.

Finding the 2.5th percentile

Or the value x in the distribution where 2.5% of the observations are below it or 97.5% of the values in the distribution are above it (100 - 2.5 = 97.5).

To solve this:

• First, find the value of z in the cumulative standard normal distribution for the probability of 2.5% or, to be more precise, 0.025.
• Second, use the formula [1].

• Third, with the values of z,
  `\\ \mu` and
  `\\ \sigma`, we solve [1] for x.
• Finally, x is the percentile asked in the question.

The first column in the cumulative standard normal distribution is the z-score with one decimal digit. The first row has the second decimal digit. Thus, we need to first find the cumulative probability of 0.025 and find the values in the first column and in the first row that corresponds to it.

These values are -1.9 and -0.06 for a cumulative probability of 0.025 or
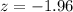`\\ z = -1.96` for
`\\ P(z<0.025)`. This is the z-score for the length at the 2.5th percentile.

Using formula [1] (without using units):

`\\ z = (x - \mu)/(\sigma)`

`\\ -1.96 = (x - 20.5)/(0.90)`

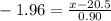
Multiplying at both sides by 0.90

`\\ -1.96*0.90 = (x - 20.5)/(0.90)*0.90`

`\\ -1.96*0.90 = (x - 20.5) * (0.90)/(0.90)`

`\\ -1.96*0.90 = (x - 20.5) * 1`

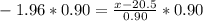
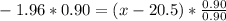
Adding 20.5 at both sides of the equation

`\\ (-1.96*0.90) + 20.5 = x - 20.5 + 20.5`

`\\ (-1.96*0.90) + 20.5 = x`

`\\ x = (-1.96*0.90) + 20.5`

`\\ x = -1.764 + 20.5`

`\\ x = 18.736 \approx 18.74`

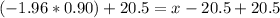
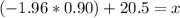
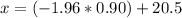
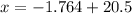
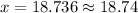
Therefore, the birth length at the 2.5th percentile is approximately 18.74 inches.

Finding the 97.5th percentile

Or the value x in the distribution where 97.5% of the observations are below it or also 0.025% of the observations in the distribution are above it (100 - 97.5 = 0.025).

We can follow the same steps as before, so:

`\\ z = (x - \mu)/(\sigma)`

Consulting the standard normal table,
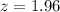`\\ z = 1.96`. This is the z-score for the 97.5th percentile.

Using [1]

`\\ z = (x - \mu)/(\sigma)`

`\\ 1.96 = (x - 20.5)/(0.90)`

`\\ (1.96 * 0.90) = x - 20.5`

`\\ (1.96 * 0.90) + 20.5 = x`

`\\ x = (1.96 * 0.90) + 20.5`

`\\ x = 1.764 + 20.5`

`\\ x = 22.264 \approx 22.26`

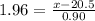
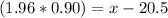
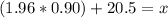
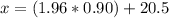
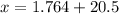
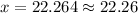
Thus, the birth length at the 97.5th percentile is about 22.26 inches.

Something worth noting is since the normal distribution is symmetrical, both percentiles are at the same distance from the mean but in diametrically opposite directions, a result taking into account the sign for z in each case (z = -1.96 and z = 1.96).

We can see these two percentiles in the below graph for a normal distribution with
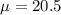`\\ \mu = 20.5` inches and
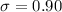`\\ \sigma = 0.90` inches. The shaded values are for
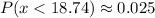`\\ P(x<18.74) \approx 0.025` (red) and
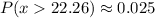`\\ P(x>22.26) \approx 0.025` (blue). Look above for the brief explanation of percentile.