Question

1. The population growth of a small town is modeled by the function P(t) = 6545.52e^0.149t where is the populationand is the number of years since 1980. A. What is the growth rate for P(t)? B. What was the population in 1980? C. Find P(11) and explain what it means in the context of the problem. D. What is the projected population in 2019?

Answer 1

A. Growth rate = r = 0.149

B. P(0) = 6545.52

C. P(11) = 33,709

D. P(39) = 2,185,876

Explanation:

The population growth of a small town is modeled by the following function,

`$ P(t) = 6545.52 e^(0.149t) $`

Where 6545.52 is the initial population, 0.149 is the rate of growth of the population and t is the number of years since 1980.

A. What is the growth rate for P(t)?

The growth rate is

Growth rate = r = 0.149

B. What was the population in 1980?

Since t is the number of years since 1980, therefore, t = 0 for the year 1980.

`P(0) = 6545.52 e^(0.149(0)) \\\\ P(0) = 6545.52 e^(0) \\\\ P(0) = 6545.52 \\\\`

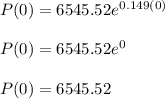
C. Find P(11) and explain what it means in the context of the problem.

`P(11) = 6545.52 e^(0.149(11)) \\\\P(11) = 6545.52 e^(1.639) \\\\ P(11) = 6545.52 (5.15) \\\\P(11) = 33,709`

It represents the population of the town after 11 years since 1980.

D. What is the projected population in 2019?

t = 2019 - 1980 = 39 years

`P(39) = 6545.52 e^(0.149(39)) \\\\P(39) = 6545.52 e^(5.811) \\\\ P(39) = 6545.52 (333.95) \\\\P(39) = 2,185,876`

Therefore, the projected population in 2019 is expected to be 2,185,876.