Answer:
Option (1)
Explanation:
Coordinates of the vertices of a quadrilateral WXYZ drawn in the figure are,
W(-1, 4), X(2, 2), Y(0, -1), Z(-3, 1)
Length of a segment having ends as
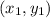 and
and
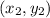 is represented by,
is represented by,
d =
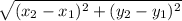
Length of WX =
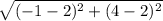
=
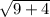
=
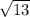
Length of XY =
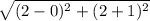
=
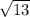
Length of YZ =
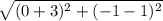
=
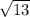
Length of ZW =
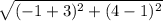
=
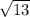
Slope of side WX (
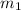 ) =
) =
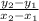
=
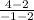
=
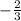
Slope of side XY (
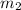 ) =
) =
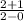
=
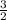
By the property of perpendicular lines,
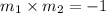
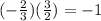
therefore, WX and XY are perpendicular.
Slope of YZ (
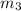 ) =
) =
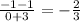
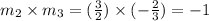
Therefore, XY ⊥ YZ
Similarly, we can prove YZ ⊥ ZW.
Therefore, quadrilateral WXYZ is a SQUARE.
Option (1) will be the answer.