Question

At a carnival, contestants are asked to keep rolling a pair of dice until they roll snake eyes. The number of rolls needed has a mean of 36 rolls, with a standard deviation of 5.4 rolls. The distribution of the number of rolls needed is not assumed to be symmetric.

Between what two numbers of rolls does Chebyshev's Theorem guarantee that we will find at least 75% of the contestants?

Answer 1

The two numbers of rolls are 25.2 and 46.8.

Explanation:

The Chebyshev's theorem states that, if X is a r.v. with mean µ and standard deviation σ, then for any positive number k, we have

`P (|X -\mu| < k\sigma) \geq (1-(1)/(k^(2)))`

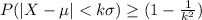
Here

`(1-(1)/(k^(2)))=0.75\\\\\Rightarrow (1)/(k^(2))=0.25\\\\\Rightarrow k=\sqrt{(1)/(0.25)}\\\\\Rightarrow k=2`

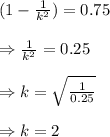
Then we know that,

`|X - \mu| \geq k\sigma,\\\\ \Rightarrow \mu - k\sigma \leq X \leq \mu + k\sigma`.

Here it is given that mean (µ) = 36 and standard deviation (σ) = 5.4.

Compute the two values between which at least 75% of the contestants lie as follows:

`P(\mu - k\sigma \leq X \leq \mu + k\sigma)=0.75\\\\P(36 - 2\cdot\ 5.4 \leq X \leq 36 + 2\cdot\ 5.4)=0.75\\\\P(25.2\leq X\leq 46.8)=0.75`

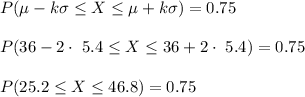
Thus, the two numbers of rolls are 25.2 and 46.8.