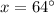Question

What is the value of angle x°?

Answer 1

`64^\circ`

Explanation:

Please refer to the attached figure for the labeling and construction in the given figure:

Given that minor angle of arc AB is
`116^\circ`.

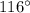Or in other words, we can say that angle subtended on the center O by the arc is
`116^\circ`.

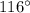Now, PA and PB are the tangents so, if we join the center of circle O with A and B, the angles formed are right angles.

i.e.

`\angle PAO = 90^\circ\\\angle PBO = 90^\circ`

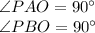
Now, we know that sum of internal angles of a quadrilateral is equal to
`360^\circ`.

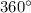Here, we have the quadrilateral AOPB.

`\therefore \angle PAO +\angle PBO+\angle AOB +\angle APB=360^\circ\\\Rightarrow 90+90+116+x=360^\circ\\\Rightarrow x = 360 - 180 - 116\\\Rightarrow x = 64^\circ`

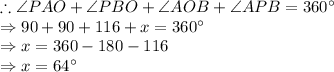
Hence, the correct answer is:

`x = 64^\circ`