Question

18 points please help pic inserted

Answer 1

1).
`\text{log}_4(5x^2+2)=\text{log}_4(x + 8)`

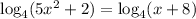
2). log(x - 1) + log5x = 2

3). ln(x + 5) = ln(x - 1) + ln(x + 1)

4).
`e^(x^2)=e^(4x+5)`

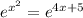
Explanation:

1). ln(x + 5) = ln(x - 1) + ln(x + 1)

ln(x + 5) = ln(x - 1)(x + 1) [Since ln(a×b) = ln a + lnb]

(x + 5) = (x- 1)(x + 1)

x + 5 = x² - 1

x² - x - 6 = 0

x² - 3x + 2x - 6 = 0

x(x - 3) + 2(x - 3) = 0

(x + 2)(x - 3 ) = 0

x = -2, 3

But x = -2 is an extraneous solution.

Therefore, x = 3 is the only solution.

2).
`e^(x^2)=e^(4x+5)`

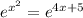
x² = 4x +5

x² - 4x - 5 = 0

x² - 5x + x - 5 = 0

x(x - 5) + 1(x - 5) = 0

(x + 1)(x - 5) = 0

x = -1, 5

Therefore, solution set is (-1, 5)

3).
`\text{log}_4(5x^2+2)=\text{log}_4(x + 8)`

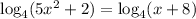
5x² + 2 = (x + 8)

5x² - x - 6 = 0

5x² - 6x + 5x - 6 = 0

x(5x - 6) + 1(5x - 6) = 0

(x + 1)(5x - 6) = 0

x = -1,
`(6)/(5)`

4). log(x - 1) + log5x = 2

log(x - 1)(5x) = 2

5x(x - 1) = 10² [if loga = b,
`a=10^(b)`]

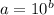5x² - 5x - 100 = 0

x² - x - 20 = 0

x² - 5x + 4x - 20 = 0

x(x - 5) + 4(x - 5) =0

(x - 5)(x + 4) = 0

x = -4, 5

But x = -4 is an extraneous solution.

Therefore, x = 5 is the only solution.