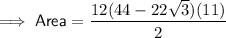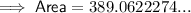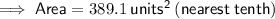Answer:
389.1 units² (nearest tenth)
Explanation:
Regular polygon: all side lengths are equal, all interior angles are equal.
Apothem: a line drawn from the center of any polygon to the midpoint of one of the sides
Radius: a line drawn from the center of the polygon to a vertex.
Therefore, we have been given the apothem of this regular dodecagon.
Formulae

where:
- n = number of sides
- l = length of one side
- a = apothem (the line drawn from the center of any polygon to the midpoint of one of the sides)

where:
- l = length of one side
- n = number of sides
Solution
First, calculate the length of one side of the regular dodecagon by substituting a = 11 and n = 12 into the apothem formula:
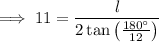
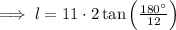
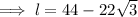
Now substitute n = 12, the found value of l, and a = 11 into the area formula: