Question

PLZ HELP!! WILL MARK BRANLYIST!!! 30 POINTS!!

Answer 1

The distance between the light and the actor's face is 29.24 ft

Explanation:

In the attached photo, you can see where the hypotenuse, the opposite side, and and adjacent side are located from the given angle measurement which is 70°. Our known side length is 10 ft which is our adjacent side and our variable is the hypotenuse. So, we will use cos.

`Cos=(adjacent)/(hypotenuse)`

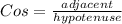
Let's plug in our numbers and variable.

`(Cos)70=(10)/(x)`

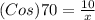
Since our hypotenuse is a variable, we are going to flip the equation so we can find the value of the hypotenuse which is also our variable.

`x=(10)/((cos)70)`

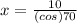
Divide 10 by (cos)70.

x = 29.24

So, the hypotenuse is 29.24 feet which shows the distance between the light and the actor's face.