Question

Given the equation A=250(1.1)t, you can determine that the interest is compounded annually and the interest rate is 10%. Suppose the interest rate were to change to being compounded quarterly. Rewrite the equation to find the new interest rate that would keep A and P the same. What is the approximate new interest rate? Convert your answer to a percentage, round it to the nearest tenth, and enter it in the space provided, like this: 42.53%

Answer 1

`r \approx 2.41\%`

Explanation:

The computation of the approximate new interest rate is shown below:

As we know that there are four quarters in a year so

The new equation is

`A = 250(1 + r)^(4t)`

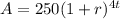
Now to determine the value of interest rate,i.e r, so place this to the first equation.

So,

`250(1.1)^(t) = 250(1 + r)^(4t)`

`1.1^(t) = (1 + r)^(4t)`

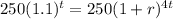
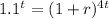
1.1 = (1 + r)^4

`\sqrt[4]{1.1} = 1 + r`

`r = -1 + \sqrt[4]{1.1}`

`r \approx 0.0241`

`r \approx 2.41\%`

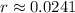
We simply applied the above formula so that the interest rate could come