Question

Answer for all please

Answer 1

a) 'X' be the random variable in discrete distribution

b) The value of y = 0.2

c) The mean value or Expectation value

E (X) = 1.25

d)

The variance σ² of the discrete distribution function is

Variance ( V(x)= 1.2875

Explanation:

Step(i):-

Given data

x : 0 1 2 3 4

P(x) : 0.30 0.35 y 0.10 0.05

a)

Let 'X' be the random variable in discrete distribution

Given data is discrete distribution

i) If the numbers
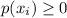`p(x_(i) )\geq 0` for all values of 'i'

ii) ∑P(x) = 1

Given data
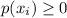`p(x_(i) )\geq 0` for all values of 'i'

∑P(x) = 1

0.30+0.35+y+0.10+0.05 =1

y + 0.8 = 1

y = 1 -0.8 = 0.2

b) The value of y = 0.2

Step(ii):-

Expectation:

Given data

x : 0 1 2 3 4

P(x) : 0.30 0.35 0.2 0.10 0.05

The mean value or Expectation value

E (x) = ∑ x p ( X = x)

= 0 × 0.30 + 1 × 0.35 + 2 × 0.2 + 3 × 0.10 + 4 × 0.05

= 0 + 0.35 + 0.4 + 0.30 + 0.2

= 1.25

Variance of X

The variance σ² of the discrete distribution function is defined by

σ² = ∑ x² p(x=x) - μ²

= 0× 0.30 + 1² × 0.35 + 2²× 0.2 +3²× 0.10 + 4²× 0.05 - (1.25)²

= 0 + 0.35 + 0.8 + 0.9 + 0.8 - 1.5625

= 1.2875

conclusion:-

The mean value or Expectation value = 1.25

The variance σ² of the discrete distribution function

V(X) = 1.2875