Answer:
Correct options:
(x – 8)² + (y – 9)² = 3
(x – 8)² + (y – 9)² = 14
Explanation:
If the circle has a center at (8,9), the equation for this circle is:
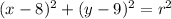
All concentric circles have the same center, so their equations need to have the same left side of the equation above.
-> x2 + y2 = 25
This circle has a center at (0,0), so it's not concentric to our circle.
-> (x – 8)² + (y – 9)² = 3
This circle has a center at (8,9), so it's concentric to our circle.
-> (x – 8)² + (y – 9)² = 14
This circle has a center at (8,9), so it's concentric to our circle.
-> (x – 8)² + (y + 9)² = 3
This circle has a center at (8,-9), so it's not concentric to our circle.
-> (x + 8)² + (y + 9)² = 25
This circle has a center at (-8,-9), so it's not concentric to our circle.
-> (x + 9)² + (y + 8)² = 3
This circle has a center at (-8,-9), so it's not concentric to our circle.
Correct options:
(x – 8)² + (y – 9)² = 3
(x – 8)² + (y – 9)² = 14