Question

The electron in a hydrogen atom, originally in level n = 8, undergoes a transition to a lower level by emitting a photon of wavelength 3745 nm. What is the final level of the electron?(c=3.00×10^8m/s, h=6.63×10^-34 J·s, RH=2.179×106-18J)a. 5

b. 6



c. 8



d. 9



e. 1

Answer 1

Step-by-step explanation:

It is given that,

The electron in a hydrogen atom, originally in level n = 8, undergoes a transition to a lower level by emitting a photon of wavelength 3745 nm. It means that,

`n_i=8`

`\lambda=3745\ nm`

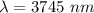
The amount of energy change during the transition is given by :

`\Delta E=R_H[(1)/(n_f^2)-(1)/(n_i^2)]`

And

`(hc)/(\lambda)=R_H[(1)/(n_f^2)-(1)/(n_i^2)]`

Plugging all the values we get :

`(6.63* 10^(-34)* 3* 10^8)/(3745* 10^(-9))=2.179* 10^(-18)[(1)/(n_f^2)-(1)/(8^2)]\\\\(5.31* 10^(-20))/(2.179* 10^(-18))=[(1)/(n_f^2)-(1)/(8^2)]\\\\0.0243=[(1)/(n_f^2)-(1)/(64)]\\\\0.0243+(1)/(64)=(1)/(n_f^2)\\\\0.039925=(1)/(n_f^2)\\\\n_f^2=25\\\\n_f=5`

So, the final level of the electron is 5.