Answer:
Side CA = 7.8
Explanation:
Given:
Acute angled
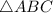 .
.
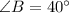
AB = 10
BC = 12
We can use cosine rule here to find the side AC = b
Formula for cosine rule:
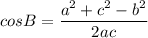
Where
a is the side opposite to

b is the side opposite to
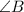
c is the side opposite to
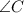
To the nearest tenth b = 7.8