Question

The average speed of a nitrogen molecule in air is about 6.70 ✕ 102 m/s, and its mass is about 4.68 ✕ 10-26 kg.(a) If it takes 3.10 ✕ 10-13 s for a nitrogen molecule to hit a wall and rebound with the same speed but moving in an opposite direction (assumed to be the negative direction), what is the average acceleration of the molecule during this time interval?Incorrect: Your answer is incorrect.Your response differs from the correct answer by more than 10%. Double check your calculations. m/s2(b) What average force does the molecule exert on the wall?

Answer 1

a = 4.32*10^15 m/s^2

Step-by-step explanation:

In order to calculate the acceleration of the nitrogen molecule, you take into account that the force experienced by the molecule, is equal to the change in its momentum:

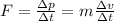`F=(\Delta p)/(\Delta t)=m(\Delta v)/(\Delta t)` (1)

m: mass of the nitrogen molecule

Δv: change in the speed of the molecule

Δt: time lapse of the change of the momentum of the molecule = 3.10*10^-13 s

Furthermore, by the Newton second law, you have:

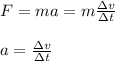`F=ma=m(\Delta v)/(\Delta t)\\\\a=(\Delta v)/(\Delta t)` (2)

The change in the speed is given by:

`\Delta v=v-v_o=6.70*10^2m/s-(-6.70*10^2m/s)=1.34*10^3(m)/(s)`

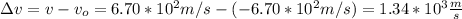
where you have taken into account the direction of the initial and final speed.

You replace the values of all parameters in the equation (1) in order to calculate the acceleration:

`a=(1.34*10^3m/s)/(3.10*10^(-13)s)=4.32*10^(15)(m)/(s^2)`

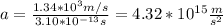
The acceleration of the nitrogen molecule is 4.32*10^15m/s^2