Answer:
First Equation → y = 21/4
Second Equation → x = -1/57
Step-by-step explanation:
solving equation #1
step 1 - simplify
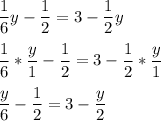
step 3 - multiply each side of the equation by six
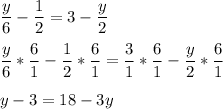
step 4 - add three to both sides of the equation.
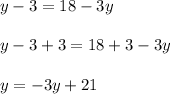
step 5 - add three y to both sides of the equation.
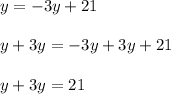
step 6 - simplify
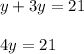
step 7 - divide both sides of the equation by four
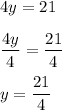
Therefore, the solution to the first given equation is y = 21/4 or y = 5.25.
solving equation #2
step 1 - simplify.
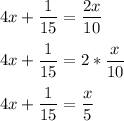
step 2 - multiply each side of the equation by five.
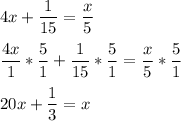
step 3 - subtract twenty x from each side of the equation.
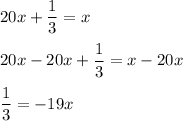
step 4 - divide each side of the equation by negative nineteen.
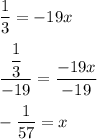
step 5 - switch
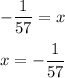
Therefore, the solution to the second equation is x = -1/57.