Answer:
The mean of the sampling distribution of sample proportions will be 0.2
Explanation:
Central Limit Theorem for Proportions:
For a proportion p in a sample of size n, the sampling distribution of the sample proportion will be approximately normal with mean
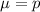 and standard deviation
and standard deviation
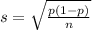
20% of American adults ages 25 and older had never been married.
This means that
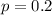
So the mean of the sampling distribution of sample proportions will be 0.2