Question

6. A distribution consists of three components with frequencies 200, 250 and 300 having means

25,10, and 15 and standard deviations 3, 4, and 5 respectively.
Calculate
The mean?
The standard deviation?​

Answer 1

The mean = 16

The standard deviation = 7.19

Step-by-step explanation:

N1 = 200 X1 = 25 σ1 = 3

N2= 250 X2 = 10 σ2 = 4

N3 = 300 X3= 15 σ3 = 5

The mean of a combined distribution is given by:

`X = (X_1N_1+X_2N_2+X_3N_3)/(N_1+N_2+N_3)\\X = (25*200+10*250+15*300)/(200+250+300)\\X=16`

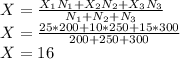
The differences from the mean for each component are:

`D_1 = 25-16=9\\D_2=10-16=-6\\D_3=15-16=-1`

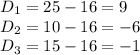
The standard deviation of a combined distribution is given by:

`\sigma=\sqrt{(N_1(\sigma_1^2+D_1^2)+N_2(\sigma_2^2+D_2^2)+N_3(\sigma_3^2+D_3^2))/(N_1+N_2+N_3)}\\\sigma=\sqrt{(200(3^2+9^2)+250(4^2+(-6)^2)+300(5^2+(-1)^2))/(200+250+300)}\\\sigma=\sqrt{(18000+13000+7800)/(750) }\\\sigma=7.19`

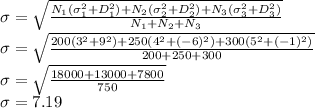
The mean = 16

The standard deviation = 7.19