Question

A cylindrical package to be sent by a postal service can have a maximum combined length and girth (perimeter of a cross section) of 141 inches. Find the dimensions of the package of maximum volume that can be sent. (The cross section is circular.)

Answer 1

Length = 47 in

Radius = 47/π in

Explanation:

Let 'h' be the length of the package, and 'r' be the radius of the cross section.

The length and girth combined are:

`L+G=141=h+2\pi r\\h=141-2\pi r`

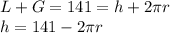
The volume of the cylindrical package is:

`V=A_b*h\\V=\pi r^2*h`

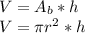
Rewriting the volume as a function of 'r':

`V=\pi r^2*h\\V=\pi r^2*(141-2\pi r)\\V=141\pi r^2-2\pi^2 r^3`

The value of 'r' for which the derivate of the volume function is zero yields the maximum volume:

`V=141\pi r^2-2\pi^2 r^3\\(dV)/(dr)=282\pi r-6\pi^2r^2=0\\ 6\pi r=282\\r=(47)/(\pi) \ in`

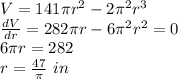
The length is:

`h=141-2\pi r=141-2\pi*(47)/(\pi)\\h=47\ in`

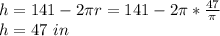
The dimensions that yield the maximum volume are:

Length = 47 in

Radius = 47/π in