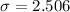Question

Consider the discrete random variable X given in the table below. Calculate the mean, variance, and standard deviation of X . Also, calculate the expected value of X . Round solution to three decimal places, if necessary. x 6 8 9 15 P ( x ) 0.64 0.14 0.14 0.08 μ = σ 2 = σ = What is the expected value of X ? E ( X )

Answer 1

Expected value or mean =
`E(x) = \mu = 7.42`

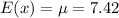
Variance =
`\sigma^2 = 6.283`

Standard deviation =
`\sigma = 2.506`

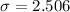
Explanation:

We are given the following information:

x | P(x)

6 | 0.64

8 | 0.14

9 | 0.14

15 | 0.08

The expected value or mean is given by

`E(x) = \mu = x \cdot P(x) \\\\E(x) = \mu = 6 \cdot 0.64 + 8 \cdot 0.14 + 9 \cdot 0.14 + 15 \cdot 0.08 \\\\E(x) = \mu = 7.42`

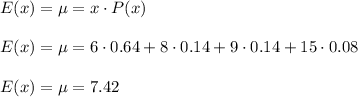
The variance is given by

`\sigma^2 = \sum (x - \mu)^2 \cdot p(x)`

`\sigma^2 = (6 - 7.42)^2 \cdot 0.64 + (8 - 7.42)^2 \cdot 0.14 + (9 - 7.42)^2 \cdot 0.14 + (15 - 7.42)^2 \cdot 0.08 \\\\\sigma^2 = 1.291 + 0.0471 + 0.349 + 4.596 \\\\\sigma^2 = 6.283`

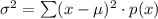
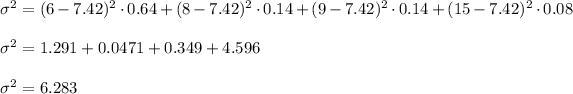
The standard deviation is given by

`\sigma = √(\sum (x - \mu)^2 \cdot p(x)) \\\\\sigma = √(\sigma^2) \\\\\sigma = √(6.283) \\\\\sigma = 2.506`

Therefore,

Expected value or mean =
`E(x) = \mu = 7.42`

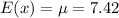
Variance =
`\sigma^2 = 6.283`

Standard deviation =
`\sigma = 2.506`