Answer:
the discount rate for this option implies to be 6.26%
Step-by-step explanation:
From the given information; we are to determine the discount rate for the cash option.
Let r represent the discount rate and
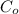 represent the cash option
represent the cash option
The the discount rate for the cash option is related to the sum of all the Present Value of the cash flows together with the discount rate.
r = discount rate = ???
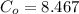 for the next 29 years.
for the next 29 years.
Mathematically;
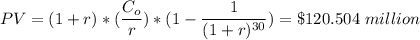
If discount rate (r) = 1%; we have:
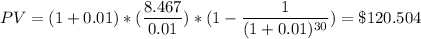

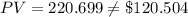
If the discount rate r= 2% ;
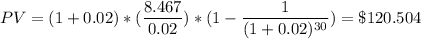
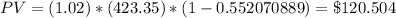
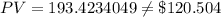
If the discount rate r= 4% ;
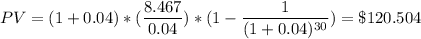
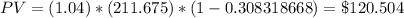
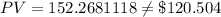
If the discount rate r = 6%

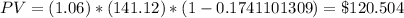
PV = 123.5396349 ≠ 120.504 (but that was so close)
If the discount rate r = 6.26%
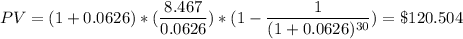
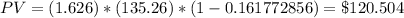
PV = 120.4722 million which is approximately equal to $120.504 million
Thus ,the discount rate for this option implies to be 6.26%