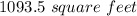Question

A farmer is building a fence to enclose a rectangular area consisting of two separate regions. The four walls and one additional vertical segment (to separate the regions) are made up of fencing, as shown below. A rectangular area consisting of two separated regions. If the farmer has 162 feet of fencing, what are the dimensions of the region which enclose the maximal areas?

Answer 1

The maximal area will be "1093.5 square feet".

Explanation:

Let,

Length = L feet

Breadth = b feet

Given Total fencing = 162 feet

According to the question,

`(2* L)+(3* b)=162`

`2L+3B=162`

`L=(162-3b)/(2)`

`L=81-(3)/(2)b`

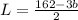
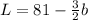
As we know,

`Area=Length* breadth`

`=(81-(3)/(2)b)* b`

`=81b-(3)/(2)b^2`

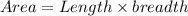
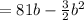
Now, we required to decrease or minimize the are. So for extreme points:

`(dA)/(db)=0`

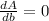
or,

`(dA)/(dB)=(d)/(db)(81-(3)/(2)b^2 )=0`

`81-(3)/(2)* 2* b=0`

`b=(81)/(3)`

`b=27 \ feet`

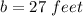
Now on putting the value of b, we get

`l=81-(3)/(2)* 27`

`=81-40.5`

`=40.5 \ feet\\`

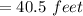
So that the dimensions will be:

⇒ 40.5 feet by 27 feet

Therefore when the dimension are above then the area will be:

=
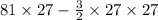
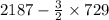
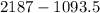
`81* 27-(3)/(2)* 27* 27`

=
`2187-(3)/(2)* 729`

=
`2187-1093.5`

=
`1093.5 \ square \ feet`