Question

The probability distribution for the number of students in statistics classes at is given, but one value is missing. Fill in the missing value, then answer the questions that follow. Round solutions to three decimal places, if necessary. x P ( x ) 23 0.08 24 0.12 25 0.15 26 27 0.1 Find the mean number of students in a Statistics class at : μ = Find the standard deviation of the number of students in a Statistics class at : σ =

Answer 1

The mean number of students in a Statistics class = 25.47

The standard deviation of the number of students in a Statistics class = 1.081.

Explanation:

We are given the following probability distribution for the number of students in statistics classes below;

X P(X)
`X * P(X)`
`X^(2) * P(X)`

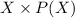
23 0.08 1.84 42.32

24 0.12 2.88 69.12

25 0.15 3.75 93.75

26 0.55 14.3 371.8

27 0.10 2.7 72.9

Total 1 25.47 649.89

The missing value against value 26 is calculated as;

= 1 - (0.08 + 0.12 + 0.15 + 0.10) = 0.55

The mean of the following data is given by;

Mean,
`\mu` =
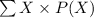`\sum X * P(X)` = 25.47

The variance of the following data is given by;

Variance,
`\sigma^(2)` =
`\sum X^(2) * P(X) - (\sum X * P(X))^(2)`

=
`649.89 - (25.47)^(2)`

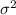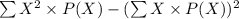
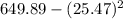
= 1.1691

Standard deviation =
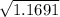`√(1.1691)` = 1.081