Question

A candle is burning. It starts out 12 inches long. After 1 hour, it is 10 inches long. After 3 hours, it is 5.5 inches

long.

1. When do you think the candle will burn out completely?

2. Is the height of the candle a function of time? If yes, is it a linear function? Explain your thinking,

Answer 1

The equation of the burning of the candle is

`y = -2x + 12`

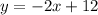
It would take 6 hours for the candle to burn out completely.

Explanation:

A candle is burning. It starts out 12 inches long.

After 1 hour, it is 10 inches long.

After 3 hours, it is 6 inches (5.5 must be a typing error)

2. Is the height of the candle a function of time? If yes, is it a linear function? Explain your thinking,

The burning of this candle can be modeled by a linear equation of the form

`y = mx + b`

where y is the length of the candle in inches, x is the time in hours, m is the slope and b is the y-intercept.

The height of the candle is clearly a function of time since it changes with time.

The slope m is given by

`$ m = (y_2 - y_1)/(x_2 - x_1) $`

Where

`(x_1, y_1) = (0, 12) \\\\(x_2, y_2) = (1, 10) \\\\`

`$ m = (10 - 12)/(1 - 0) $`

`m = -2`

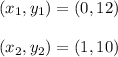
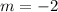
The slope of negative 2 means that the length of the canlde is decreasing by a factor of 2.

To find the value of the y-intercept (b),

substitute (x, y) = (0, 12)

which means that at x = 0 the length of the candle is 12 inches.

`y = mx + b \\\\12 = -2(0) + b \\\\b = 12`

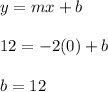
So the equation of burning of the candle becomes

`y = mx + b \\\\y = -2x + 12 \\\\`

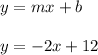
1. When do you think the candle will burn out completely?

Since we have the equation now we can find the length of the candle for any given time and also find the time required for a specific length of the candle.

Burn out completely means the length of the candle becomes zero.

`y = -2x + 12 \\\\0 = -2x + 12 \\\\-2x = -12 \\\\x = 12/2 \\\\x = 6 \: hours \\\\`

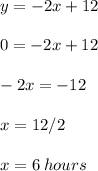
Therefore, it would take 6 hours for the candle to burn out completely.