Question

A company plan to manufacture closed rectangular boxes that have a volume of 8m3

. If the

material for the top and bottom costs twice as much as the material for the sides. Find the

dimensions that will minimize the cost.​

Answer 1

Base Side Length =1.59m

Height = 3.16 m

Explanation:

Volume of the box =
`8$ m^3`

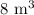
Let the base dimensions = x and y

Let the height of the box =h

However, for any optimal configuration, Width = Length as varying the length and width to be other than equal reduces the volume for the same total(w+l)

Volume, V=xyh=8

Since x=y

`h=(8)/(x^2)`

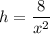
Surface Area of the box

`= 2(x^2+xh+xh)\\=2x^2+4xh`

The material for the top and bottom costs twice as much as the material for the sides.

Let the cost of the sides =$1 per square meter

Cost of the material for the sides = 4xh

Cost of the material for the top and bottom =
`=2*2x^2=4x^2`

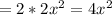
Therefore:

Total Cost,
`C= 4xh+4x^2`

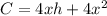
Substitution of
`h=(8)/(x^2)` into C

`C= 4x((8)/(x^2))+4x^2\\=(32)/(x)+4x^2\\C(x)=(4x^3+32)/(x)`

To minimize C(x), we find its derivative and solve for the critical points.

`C'(x)=(8x^3-32)/(x^2)\\$Setting C'(x) to zero\\8x^3-32=0\\8x^3=32\\x^3=4\\x=\sqrt[3]{4}\\ x=1.59$ m`

To verify if it is a minimum, we use the second derivative test

`C''(x)=8+(64)/(x^3)\\C''(1.59)=23.92`

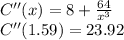
Since C''(x) is greater than zero, it is a minimum point.

Recall:

`h=(8)/(x^2)\\h=(8)/(1.59^2)=3.16$ m`

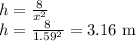
Therefore, the dimensions that minimizes the cost are:

Base Side Lengths of 1.59m; and

Height of 3.16 m