The length of JL is approximately 15.87 units.
To find the length of JL, we can use the Pythagorean theorem.
In triangle △JKL, ∠JKL is a right angle, and KM is an altitude.
Since JK=24 and JM=18, we can use these lengths to find JL.
Let's label the length of JL as x.
Using the Pythagorean theorem, we have:
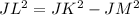
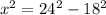
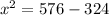
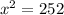
x = √252
Therefore, the length of JL is approximately 15.87 units.