Answer:
The answer is explained below
Explanation:
The location of point A = (-5, -1) and point B = (4, 1).
To find the coordinate of the point that divides a line segment PQ with point P at
 and point Q at
and point Q at
 in the proportion a:b, we use the formula for the x and y coordinates:
in the proportion a:b, we use the formula for the x and y coordinates:
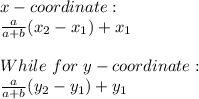
P is One-fourth the length of the line segment from A to B, Therefore AB is divided in the ratio 1:4. The location of point A = (-5, -1) and point B = (4, 1).Therefore:
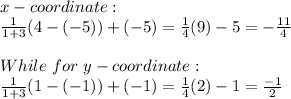
Therefore the coordinate of P is (-11/4, -1/2)