Question

In an undergraduate physics lab, a simple pendulum is observed to swing through 71 complete oscillations in a time period of 1.80 min. What are the period and length of the pendulum

Answer 1

Step-by-step explanation:

We have

A simple pendulum is observed to swing through 71 complete oscillations in a time period of 1.80 min.

The frequency of a pendulum is equal to the no of oscillation per unit time. so,

`f=(N)/(t)\\\\f=(71)/(1.8* 60)\\\\f=0.65\ Hz`

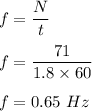
Tim period is reciprocal of frequency. So,

`T=(1)/(0.65)\\\\T=1.53\ s`

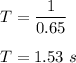
The time period of a pendulum is given by :

`T=2\pi \sqrt{(l)/(g)}`

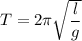
l is length of pendulum

`l=(T^2g)/(4\pi ^2)\\\\l=(T^2g)/(4\pi ^2)\\\\l=((1.53)^2* 9.8)/(4\pi ^2)\\\\l=0.58\ m`

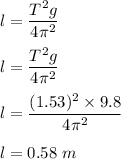
So, the period and length of the pendulum are 1.53 s and 0.58 m respectively.