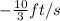Question

g A 5 foot tall man walks at 10 ft/s toward a street light that is 20 ft above the ground. What is the rate of change of the length of his shadow when he is 25 ft from the street light

Answer 1

`-(10)/(3)ft/s`

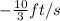
Explanation:

We are given that

Height of man=5 foot

`(dy)/(dt)=-10ft/s`

Height of street light=20ft

We have to find the rate of change of the length of his shadow when he is 25 ft form the street light.

ABE and CDE are similar triangle because all right triangles are similar.

`(20)/(5)=(x+y)/(x)`

`4=(x+y)/(x)`

`4x=x+y`

`4x-x=y`

`3x=y`

`3(dx)/(dt)=(dy)/(dt)`

`(dx)/(dt)=(1)/(3)(-10)=-(10)/(3)ft/s=-(10)/(3)ft/s`

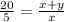
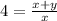
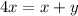
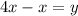
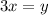
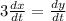
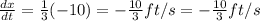
Hence, the rate of change of the length of his shadow when he is 25 ft from the street light=
`-(10)/(3)ft/s`