Question

A sample of 17 patients in a hospital had these hemoglobin readings 112 120 98 55 71 35 99 142 64 150 150 55 100 132 20 70 93 find a 95% confidence interval for the hemoglobin reading for all the patienta in the hospital​

Answer 1

The 95% confidence interval for the hemoglobin reading for all the patients in the hospital is (72, 112).

Explanation:

The (1 - α)% confidence interval for the population mean, when the population standard deviation is not provided is:

`CI=\bar x\pm t_(\alpha/2, (n-1))\cdot (s)/(√(n))`

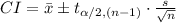
The data provided is:

S = {112, 120, 98, 55, 71, 35, 99, 142, 64, 150, 150, 55, 100, 132, 20, 70, 93}

Compute the sample mean and sample standard deviation as follows:

`\bar x=(1)/(n)\sum X=(1)/(17)*[112+120+98+...+93]=92.1176\\\\s=\sqrt{(1)/(n-1)\sum (x-\bar x)^(2)}=\sqrt{(1)/(17-1)* 25041.7647}=39.56`

The critical value of t for 95% confidence level and n - 1 = 16 degrees of freedom is:

`t_(\alpha/2, (n-1))=t_(0.05/2, 16)=2.120`

*Use a t-table.

Compute the 95% confidence interval for the hemoglobin reading for all the patients in the hospital as follows:

`CI=\bar x\pm t_(\alpha/2, (n-1))\cdot (s)/(√(n))`

`=92.1176\pm 2.120*(39.56)/(√(17))\\\\=92.1176\pm 20.3408\\\\=(71.7768, 112.4584)\\\\\approx (72, 112)`

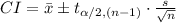
Thus, the 95% confidence interval for the hemoglobin reading for all the patients in the hospital is (72, 112).