Answer:
The simplified expressions are (x + y·z' + t) and x·(x + y' + z) respectively.
Explanation:
The expressions provided are:
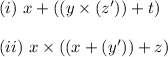
(i)
Simplify the first expression with as few symbols as possible:
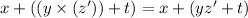
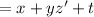
(ii)
Simplify the second expression with as few symbols as possible:
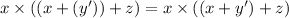
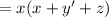
Thus, the simplified expressions are (x + y·z' + t) and x·(x + y' + z) respectively.