Question

An aluminum bar 600mm long, with diameter 40mm, has a hole drilled in the center of the bar. The hole is 40mm in diameter and 100mm long. If modulus of elasticity is for the aluminum is 85GN/m^2, calculate the total contraction on the bar due to compressive load of 180kN?

Answer 1

1.228 x
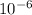`10^(-6)` mm

Step-by-step explanation:

diameter of aluminium bar D = 40 mm

diameter of hole d = 30 mm

compressive Load F = 180 kN = 180 x
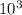`10^(3)` N

modulus of elasticity E = 85 GN/m^2 = 85 x
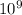`10^(9)` Pa

length of bar L = 600 mm

length of hole = 100 mm

true length of bar = 600 - 100 = 500 mm

area of the bar A =
`(\pi D^(2) )/(4)` =
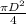`(3.142* 40^(2) )/(4)` = 1256.8 mm^2

area of hole a =
`(\pi(D^(2) - d^(2)) )/(4)` =
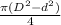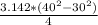`(3.142*(40^(2) - 30^(2)))/(4)` = 549.85 mm^2

Total contraction of the bar =
`(F*L)/(AE) + (Fl)/(aE)`

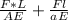
total contraction =
`(F)/(E) * ((L)/(A) +(l)/(a))`

==>
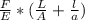
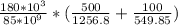`(180*10^(3))/(85*10^(9)) *( (500)/(1256.8) + (100)/(549.85))` = 1.228 x
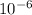`10^(-6)` mm