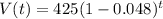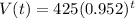Answer:
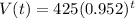
Explanation:
The amount of water in the bucket after t hours, in mL, can be modeled by an equation in the following format:

In which V(0) is the initial amount, and r is the constant decay rate, as a decimal.
Bucket contains 425 mL of water.
This means that
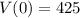
The capacity of water in the bucket decreases 4.8% each hour.
This means that
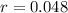
So