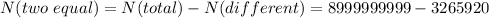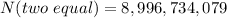Question

How many ten-digit numbers have at least two equal digits?

Answer 1

8,996,734,079 numbers

Explanation:

First let's find the number of ten-digit numbers.

The maximum ten-digit number is 9,999,999,999 and the minimum is 1,000,000,000. So the number of ten-digit numbers is:

`N(total) = 9999999999 - 1000000000 = 8,999,999,999`

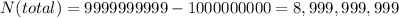
Now, to find the number of ten-digit numbers with at least two equal digits, we can find the number of ten-digit numbers with all digits different, and then subtract this amount from the total ten-digit numbers.

To find the number of ten-digit numbers with all digits different, we can use the following logic:

The first digit can have 9 different values (0 not included), the second can also have 9 (one digit used), then the third can have 8 (two digits used), the fourth can have 7, and so on. So we have that:

`N(different) = 9*9! = 3,265,920`

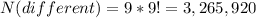
Then the number of ten-digit numbers with at least two equal digits is:

`N(two\ equal) = N(total)-N(different) = 8999999999 - 3265920`

`N(two\ equal) = 8,996,734,079`