Answer:
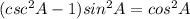
We know that
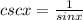 and using this identity we have:
and using this identity we have:
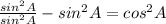
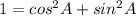
And if we remember the equation above represent the fundamental identity in trigonometry and is satisfied for every real number and we can say that the solution for this case is:
![A= [X | x \in R]](https://img.qammunity.org/2021/formulas/mathematics/college/k17q5xbyla5ikww6739ukqm2df98u8an31.png)
Explanation:
For this case we have the following equation given:
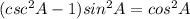
We know that
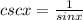 and using this identity we have:
and using this identity we have:
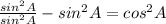
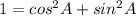
And if we remember the equation above represent the fundamental identity in trigonometry and is satisfied for every real number and we can say that the solution for this case is:
![A= [X | x \in R]](https://img.qammunity.org/2021/formulas/mathematics/college/k17q5xbyla5ikww6739ukqm2df98u8an31.png)