Question

A 6.00kg box is subjected to a force F=18.0N-(0.530N/m)x. Ignoring friction and using Work, find the speed of the box after it has traveled 14.0m from rest

Answer 1

Approximately
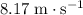`8.17\; \rm m \cdot s^(-1)` assuming that the effect of gravity on the box can be ignored.

Step-by-step explanation:

If the force
`F` is constant, then the work would be found with
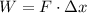`W = F \cdot \Delta x`. However, this equation won't work for this question since the

`\displaystyle W = \int\limits_(x_0)^(x_1) F\, d x`,

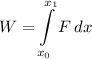For this particular question,
`x_0 = 0\; \rm m` and
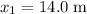`x_1 = 14.0\; \rm m`. Apply this equation:

`\begin{aligned}W &= \int\limits_(x_0)^(x_1) F\, d x \\ &= \int\limits_(0\; \rm m)^(14.0\; \rm m) \left[{18.0\; \rm N} - {\left(0.530\; {\rm N \cdot m^(-1)}\right)}\cdot x \right]\, d x \\ &= \left[{(18.0\; \rm N)}\cdot x - (1)/(2)\;{\left(0.530\; {\rm N \cdot m^(-1)}\right)}\cdot x^2\right]_(x = 0\; \rm m)^(x = 14.0\; \rm m) \approx 200.06\; \rm N \cdot m\end{aligned}`.

(Side note: keep in mind that
`1\; \rm J = 1\; \rm N\cdot m`.)

Since friction is ignored, all these work should have been converted to the mechanical energy of this object.

Assume that the effect of gravity on this box can also be ignored. That way, there won't be a change in the gravitational potential energy of this object. Hence, all these extra mechanical energy would be in the form of the kinetic energy of this box.

That is:

`\begin{aligned}& \text{Kinetic energy of this object} \\ =& \text{Initial Kinetic Energy} + \text{Change in Kinetic Energy} \\ =& \text{Initial Kinetic Energy} + \text{Change in Mechanical Energy} \\ =& \text{Initial Kinetic Energy} + \text{External Work} \\=& 0\; \rm N \cdot m + 200.06\; \rm N \cdot m \\ =& 200.06\; \rm N \cdot m \end{aligned}`.

Keep in mind that the kinetic energy of an object of mass
`m` and speed
`v` is:

`\displaystyle (1)/(2)\, m \cdot v^(2)`.

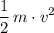Therefore:

`\begin{aligned}v &= \sqrt{\frac{2\, (\text{Kinetic energy})}{m}} \\ &= \sqrt{(2* 200.06\; \rm N \cdot m)/(6.00\; \rm kg)} \approx 8.17\; \rm m \cdot s^(-1)\end{aligned}`.