Question

What is the leading coefficient of a cubic polynomial that has a value of −208 when x=1, and has zeros of 5, 5i, and −5i?

Answer 1

2

Explanation:

We already have the zeros, so we can write the cubic polynomial in this general form:

`y = a(x - x_1)(x - x_2)(x - x_3)`

Where:

`x_1 = 5`

`x_2 = 5i`

`x_3 = -5i`

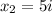
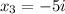
So we have that:

`y = a(x -5)(x - 5i)(x + 5i)`

`y = a(x -5)(x^2 + 25)`

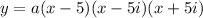
To find the value of the leading coefficient 'a', we can use the point (1, -208) given:

`-208 = a(1 -5)(1 + 25)`

`-208 = a(-4)(26)`

`a = -208 / (-104) = 2`

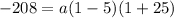
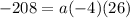
So the leading coefficient is 2.