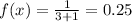Answer:
a)
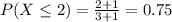
b)

c)
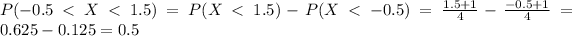
d)
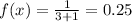
Explanation:
Let X the random variable of interest and we know that the distribution is given by:
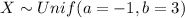
And for this problem we can use the cumulative distribution function in order to solve the items:
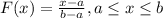
Part a
We want to find this probability:
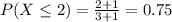
Part b

Part c
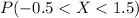
And we can calculate the probability with this difference:
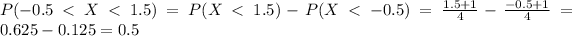
Part d
Since we have a continuous distribution the the probability for an unique value would be: