Question

What is the nth term rule of the quadratic sequence below? 4,15,30,49,72,99,130,...

Answer 1

The nth term rule of the quadratic sequence is
`2n^(2) +5n-3`.

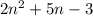Explanation:

We are given the following quadratic sequence below;

4, 15, 30, 49, 72, 99, 130,...

As we know that the formula for the nth term of the quadratic sequence is given by =
`an^(2)+bn+c`

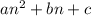
Firstly, we will find the difference between the term of the given sequence;

1st difference of the given sequence;

(2nd term - 1st term), (3rd term - 2nd term), (4th term - 3rd term), (5th term - 4th term), (6th term - 5th term), (7th term - 6th term)

= (15 - 4), (30 - 15), (49 - 30), (72 - 49), (99 - 72), (130 - 99),....

= (11, 15, 19, 23, 27, 31,.....)

Now, we will find the second difference of the given sequence, i.e;

= (15 - 11), (19 - 15), (23 - 19), (27 - 23), (31 - 27),....

= (4, 4, 4, 4, 4)

Since the differences are same now, so to find the value of a we have to divide the value of second difference by 2, i.e;

The value of a =
`(4)/(2)` = 2

SO, the first term of the nth term rule equation is
`an^(2)` =
`2n^(2)`.

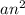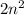Now, in the term
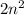`2n^(2)`, put the value of n = 1, 2, 3, 4 and 5 and then form the sequence, i.e;

If n = 1, then
`2n^(2)` =
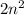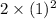`2 * (1)^(2)` = 2

If n = 2, then
`2n^(2)` =
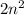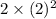`2 * (2)^(2)` = 8

If n = 3, then
`2n^(2)` =
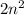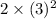`2 * (3)^(2)` = 18

If n = 4, then
`2n^(2)` =
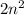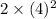`2 * (4)^(2)` = 32

If n = 5, then
`2n^(2)` =
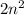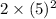`2 * (5)^(2)` = 50

SO, the sequence formed is (2, 8, 18, 32, 50).

Now, find the difference of this sequence and the original quadratic sequence, i.e;

= (4 - 2), (15 - 8), (30 - 18), (49 - 32), (72 - 50)

= (2, 7, 12, 17, 22)

Now, as we can see that the above sequence resembles the general form of (5n - 3) because:

If we put n = 1, then (5n - 3) = 5 - 3 = 2

If we put n = 2, then (5n - 3) = 10 - 3 = 7 and so on....

From this, we concluded that the value of b and c are 5 and (-3) respectively.

Hence, the nth term rule for the given quadratic sequence is
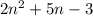`2n^(2) +5n-3`.