Question

Fredrick hit 14, 18, 13, 12, 12, 16, 13, 12, 1, and 15 home runs in 10 seasons of play. Which statements are correct? Check all that apply. Fredrick’s data set contains an outlier. The median value is 12 home runs. The mean value is about 12.6 home runs. The median describes Fredrick’s data more accurately than the mean. The mean value stays the same when the outlier is not included in the data set.

Answer 1

(a) Yes, Fredrick’s data set contains an outlier.

(b) No, the median value is not 12 home runs.

(c) Yes, the mean value is about 12.6 home runs.

(d) Yes, the median describes Fredrick’s data more accurately than the mean.

(e) No, the mean value doesn't stay the same when the outlier is not included in the data set.

Explanation:

We are given that Fredrick hit 14, 18, 13, 12, 12, 16, 13, 12, 1, and 15 home runs in 10 seasons of play.

Firstly, arranging our data set in ascending order we get;

1, 12, 12, 12, 13, 13, 14, 15, 16, 18.

(a) The statement that Fredrick’s data set contains an outlier is true because in our data set there is one value that stands out from the rest of the data, which is 1.

Hence, the outlier value in the data set is 1.

(b) For calculating median, we have to first observe that the number of observations (n) in the data set is even or odd, i.e;

• If n is odd, then the formula for calculating median is given by;

Median =
`((n+1)/(2))^(th) \text{ obs.}`

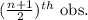
• If n is odd, then the formula for calculating median is given by;

Median =
`\frac{((n)/(2))^(th) \text{ obs.}+((n)/(2)+1)^(th) \text{ obs.} }{2}`

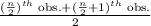
Here, the number of observations in Fredrick's data set is even, i.e. n = 10.

SO, Median =
`\frac{((n)/(2))^(th) \text{ obs.}+((n)/(2)+1)^(th) \text{ obs.} }{2}`

=
`\frac{((10)/(2))^(th) \text{ obs.}+((10)/(2)+1)^(th) \text{ obs.} }{2}`

=
`\frac{(5)^(th) \text{ obs.}+(6)^(th) \text{ obs.} }{2}`

=
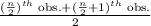
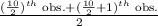
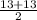`(13+13 )/(2)` = 13 home runs

So, the statement that the median value is 12 home runs is not correct.

(c) The mean of the data set is given by;

Mean =
`(1+ 12+ 12+ 12+ 13+ 13+14+ 15+ 16+ 18)/(10)`

=
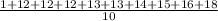
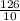`(126)/(10)` = 12.6 home runs

So, the statement that the mean value is about 12.6 home runs is correct.

(d) The statement that the median describes Fredrick’s data more accurately than the mean is correct because even if the outlier is removed from the data set, the median value will remain unchanged but the mean value gets changed.

(e) After removing the outlier, the data set is;

12, 12, 12, 13, 13, 14, 15, 16, 18.

Now, the mean of the data =
`(12+12+ 12+ 13+ 13+ 14+ 15+ 16+ 18)/(9)`

=
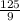`(125)/(9)` = 13.89

So, the statement that the mean value stays the same when the outlier is not included in the data set is incorrect.