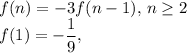Question

The explicit formula for the geometric sequence Negative one-ninth, one-third, negative 1, 3, negative 9, ellipsis is f (x) = negative one-ninth (negative 3) Superscript x minus 1. What is the common ratio and recursive formula for this sequence?

Answer 1

It is in fact B. −3; f(x + 1) = −3(f(x))

Explanation:

If you have this question on Edge, go with this.

Answer 2

Common ratio, r=-3

Recursive Formula

`f(n)=-3f(n-1),$ $n\geq 2\\f(1)=-(1)/(9),`

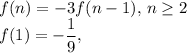
Explanation:

The formula for the geometric sequence:
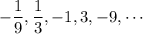`-(1)/(9) ,(1)/(3), -1,3,-9,\cdots` is given as:

`f(x)=-(1)/(9)(-3)^(x-1)`

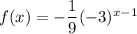
Common Ratio

Dividing the next terms by the previous terms, we obtain:

`(1)/(3) / -(1)/(9) = (1)/(3) * -9 =-3\\3 / -1 =-3\\-9 / 3 =-3`

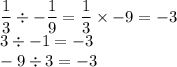
Therefore, the common ratio of the sequence, r=-3

Recursive Formula

We observe that the next term,
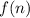`f(n)` is obtained by the multiplication of the previous term. f(n-1) by -3.

Therefore, a recursive formula for the sequence is:

`f(n)=-3f(n-1),$ $n\geq 2\\f(1)=-(1)/(9),`