Answer:
The speed of the object is (
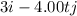 )m/s
)m/s
The magnitude of the acceleration is 4.00m/s²
Step-by-step explanation:
Given - position vector;
r = (2.0 + 3.00t)i + (3.0 - 2.00t²)j -------------------(i)
To get the speed vector (
 ), take the first derivative of equation (i) with respect to time t as follows;
), take the first derivative of equation (i) with respect to time t as follows;
 =
=
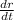
 =
=
![(d[(2.0 + 3.00t)i + (3.0 - 2.00t^2)j] )/(dt)](https://img.qammunity.org/2021/formulas/physics/college/ax5ba4f8hqhupph6xztdvu7oxvm6jhxx6j.png)
 =
=
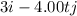 ------------------------(ii)
------------------------(ii)
To get the acceleration vector (
 ), take the first derivative of the speed vector in equation(ii) as follows;
), take the first derivative of the speed vector in equation(ii) as follows;
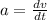
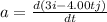
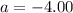 j
j
The magnitude of the acceleration |a| is therefore given by
|a| = |-4.00|
|a| = 4.00 m/s²
In conclusion;
the speed of the object is (
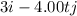 )m/s
)m/s
the magnitude of the acceleration is 4.00m/s²