Answer:
A
Explanation:
Given a parabola in standard form, y = ax² + bx + c ( a ≠ 0 ), then
minimum/ maximum value is the y- coordinate of the vertex.
The x- coordinate of the vertex is
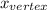 = -
= -
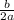
y = x² -
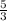 x +
x +
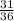 ← is in standard form
← is in standard form
with a = 1 and b = -
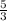 , thus
, thus
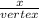 = -
= -
 =
=

Substitute this value into y
y = (
 )² -
)² -
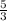 (
(
 ) +
) +
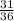
=
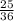 -
-
 +
+
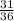 =
=

Since a > 1 then the vertex is a minimum, thus
minimum value =
 → A
→ A