Question

Find the x-intercepts of the parabola with vertex (4,-1) and y-intercept (0,15). Write your answer in this form: (x1,y1),(x2,y2). If necessary, round to the nearest hundredth.

Answer 1

(3,0) and (5,0)

Explanation:

First let's write the generic model of a parabola:

`y = ax^2 + bx + c`

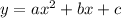
Now, using the points (0, 15) and (4, -1), we have:

(0, 15):

`15 = 0a + 0b + c`

`c=15`

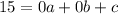
(4, -1):

`-1 =16a+4b+15`

`16a + 4b = -16`

`4a + b = -4`

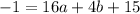
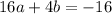
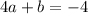
The x-coordinate of the vertex is given by the equation:

`x_v = -b/2a`

`-b/2a = 4`

`b = -8a`

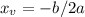
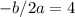
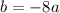
Now, using this value of b in the equation
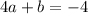`4a + b = -4`, we have:

`4a - 8a = -4`

`a = 1`

`b = -8`

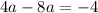
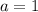
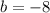
The x-intercepts are where we have y = 0, so:

`0 = x^2 -8x + 15`

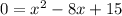
Using Bhaskara's formula, we have:

`\Delta = b^2 - 4ac = 64 -60 = 4`

`x = -b \±√(\Delta)/2a`

`x_1 = (8 + 2)/2 = 5`

`x_2 = (8 - 2)/2 = 3`

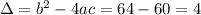
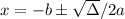
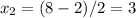
So the x-intercepts are (3,0) and (5,0).