Question

Fred the ant is on the real number line, and Fred is trying to get to the point 0. If Fred is at 1, then on the next step, Fred moves to either 0 or 2 with equal probability. If Fred is at 2, then on the next step, Fred always moves to 1. Let e_1 be expected number of steps Fred takes to get to 0, given that Fred starts at the point 1. Similarly, let e_2 be expected number of steps Fred takes to get to 0, given that Fred starts at the point 2. Determine the ordered pair (e_1,e_2). Answer is NOT (2, 3)

Answer 1

(3, 4)

Explanation:

For e_1, there is first a 1/2 chance that Fred will go to point 0 on the first move, giving us an expected value of 1/2. Similarily, there is 1/4 chance that Fred will go to point 0 on the 3rd move, giving us an expected value of 3/4th moves. We continue, and we see that the expected value for the number of moves is this.

`1/2 + 3/4 + 5/8 + 7/16 + 9/32 + 11/64 ...`

This equation eventually equals to 3, so e_1 is equal to 3.

For e_2, it's just e_1 + 1, because Fred has to move to point 1 in the first place.

Answer 2

The ordered pair (e₁, e₂) is (6, 8).

Explanation:

Consider the pathway attached below.

• Consider that Fred is at 1.

It is provided that Fred moves to either 0 or 2 with equal probability, i.e. 0.50.

e₁ : 1 3 5 7 ...

P (e₁) : 0.50 0.50² 0.50³ 0.50⁴ ...

The expected number of steps Fred takes to get to 0 if he is at 1 is:

`e_(1)=(1* 0.50)+(3* 0.50^(2))+(5* 0.50^(3))+(7* 0.50^(4))+...\\\\`

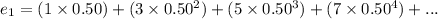
The sum series e₁ is an AGP.

The sum of infinite AGP is:
`(a)/(1-r)+(dr)/((1-r)^(2))`

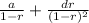
Then the value of e₁ is:

`e_(1)=(1)/((1-0.50))+(2* 0.50)/((1-0.50)^(2))\\\\=2+4\\\\=6`

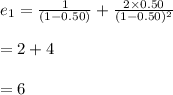
• Consider that Fred is at 2.

It is provided that Fred always moves to 1 if he at step 2.

e₂ : 2 4 6 8 ...

P (e₂) : 0.50 0.50² 0.50³ 0.50⁴ ...

The expected number of steps Fred takes to get to 0 if he is at 2 is:

`e_(2)=(2* 0.50)+(4* 0.50^(2))+(6* 0.50^(3))+(8* 0.50^(4))+...\\\\`

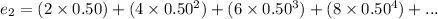
The sum series e₂ is an AGP.

The sum of infinite AGP is:
`(a)/(1-r)+(dr)/((1-r)^(2))`

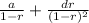
Then the value of e₂ is:

`e_(1)=(2)/((1-0.50))+(2* 0.50)/((1-0.50)^(2))\\\\=4+4\\\\=8`

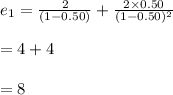
Thus, the ordered pair (e₁, e₂) is (6, 8).