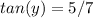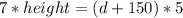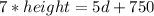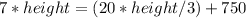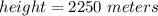Question

From a point on the ground the angle of elevation of the top of a tower is x°. Moving 150 meters away from that point the angle of elevation was found to be y° .If tan x=3/4 and tan y=5/7 find the height of the tower.​

Answer 1

The height of the tower is 2250 meters

Explanation:

let's say that when the angle of elevation is x°, the distance to the base of the tower is 'd'. So when the angle of elevation is y°, the distance is d+150.

The tangent of the angle of elevation is the height of the tower (opposite side) over the horizontal distance to the tower (adjacent side).

Then we have that:

angle of elevation x°:

`tan(x) = 3/4`

`height / d = 3/4`

`d = (4/3)*height`

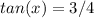
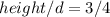
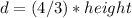
angle of elevation y°:

`tan(y) = 5/7`

`height / (d+150) = 5/7`

`7*height = (d+150) * 5`

`7*height = 5d+750`

`7*height = (20*height/3)+750`

`21*height = 20*height+2250`

`height = 2250\ meters`