Question

Here are two squares, A and B.

A

B

The length of the side of square A is 50% of the length of the side of square B.

Express the area of the shaded region of square A

as a percentage of the area of square B.

otal marks: 3

Submit Answer

Answer 1

The two squares and the shaded region of square A is in the attachment.

Answer: The shaded region of A is 12.5% of the area of B.

Step-by-step explanation: Assume that the length of side of square A is a and the length of side of square B is b.

Length a is half (50%) of length b:

a =
`(b)/(2)`

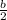
The shaded region is a triangle. The area of a triangle is: A =
`(b.h)/(2)`

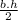
b and h are the sides of the square A, so:

`A_(1)` =
`((b)/(2).(b)/(2))/(2)`

`A_(1) = (b)/(2).(b)/(2).(1)/(2)`

`A_(1) = (b^(2))/(8)`

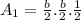
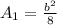
Area of square B is:

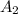`A_(2)` = b.b

`A_(2) = b^(2)`

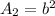
Comparing areas:

`((b^(2))/(8) )/(b^(2))` =
`(b^(2))/(8).(1)/(b^(2))` =
`(1)/(8)`

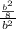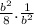As percentage:

`(1)/(8)` × 100 = 0.125 × 100 = 12.5%

Comparing the shaded region of A to square B, the area of the first is 12.5% smaller than the second.