Question

Use the substitution x = 2 − cos θ to evaluate the integral ∫ 2 3/2 ( x − 1 3 − x )1 2 dx. Show that, for a < b, ∫ q p ( x − a b − x )1 2 dx = (b − a)(π + 3√ 3 − 6) 12 , where p = ???????????????????????????

Answer 1

If the integral as written in my comment is accurate, then we have

`I=\displaystyle\int_(3/2)^2√((x-1)(3-x))\,\mathrm dx`

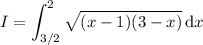
Expand the polynomial, then complete the square within the square root:

`(x-1)(3-x)=-x^2+4x-3=1-(x-2)^2`

`I=\displaystyle\int_(3/2)^2√(1-(x-2)^2)\,\mathrm dx`

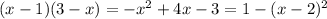
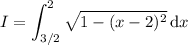
Let
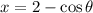`x=2-\cos\theta` and
`\mathrm dx=\sin\theta\,\mathrm d\theta`:

`I=\displaystyle\int_(\pi/3)^(\pi/2)√(1-(2-\cos\theta-2)^2)\sin\theta\,\mathrm d\theta`

`I=\displaystyle\int_(\pi/3)^(\pi/2)√(1-\cos^2\theta)\sin\theta\,\mathrm d\theta`

`I=\displaystyle\int_(\pi/3)^(\pi/2)√(\sin^2\theta)\sin\theta\,\mathrm d\theta`

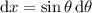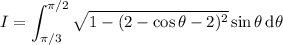
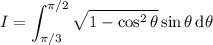
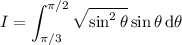
Recall that
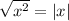`√(x^2)=|x|` for all
`x`, but for all
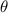`\theta` in the integration interval we have
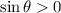`\sin\theta>0`. So
`√(\sin^2\theta)=\sin\theta`:

`I=\displaystyle\int_(\pi/3)^(\pi/2)\sin^2\theta\,\mathrm d\theta`

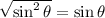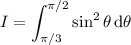
Recall the double angle identity,

`\sin^2\theta=\frac{1-\cos(2\theta)}2`

`I=\displaystyle\frac12\int_(\pi/3)^(\pi/2)(1-\cos(2\theta))\,\mathrm d\theta`

`I=\frac\theta2-\frac{\sin(2\theta)}4\bigg|_(\pi/3)^(\pi/2)`

`I=\frac\pi4-\left(\frac\pi6-\frac{\sqrt3}8\right)=\boxed{\frac\pi{12}+\frac{\sqrt3}8}`

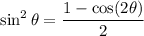
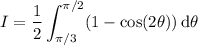
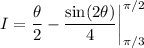
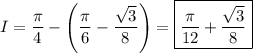
You can determine the more general result in the same way.

`I=\displaystyle\int_p^q√((x-a)(b-x))\,\mathrm dx`

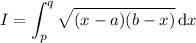
Complete the square to get

`(x-a)(b-x)=-(x-a)(x-b)=-x^2+(a+b)x-ab=\frac{(a+b)^2}4-ab-\left(x-\frac{a+b}2\right)^2`

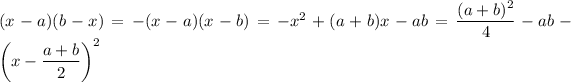
and let
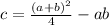`c=\frac{(a+b)^2}4-ab` for brevity. Note that

`c=\frac{(a+b)^2}4-ab=\frac{a^2-2ab+b^2}4=\frac{(a-b)^2}4`

`I=\displaystyle\int_p^q\sqrt{c-\left(x-\frac{a+b}2\right)^2}\,\mathrm dx`

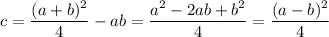
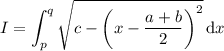
Make the following substitution,

`x=\frac{a+b}2-\sqrt c\,\cos\theta`

`\mathrm dx=\sqrt c\,\sin\theta\,\mathrm d\theta`

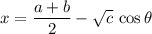
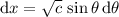
and the integral reduces like before to

`I=\displaystyle\int_P^Q√(c-c\cos^2\theta)\,\sin\theta\,\mathrm d\theta`

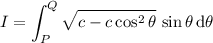
where

`p=\frac{a+b}2-\sqrt c\,\cos P\implies P=\cos^(-1)\frac{\frac{a+b}2-p}{\sqrt c}`

`q=\frac{a+b}2-\sqrt c\,\cos Q\implies Q=\cos^(-1)\frac{\frac{a+b}2-q}{\sqrt c}`

`I=\displaystyle\frac{\sqrt c}2\int_P^Q(1-\cos(2\theta))\,\mathrm d\theta`

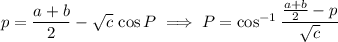
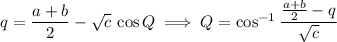
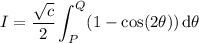
(Depending on the interval [p, q] and thus [P, Q], the square root of cosine squared may not always reduce to sine.)

Resolving the integral and replacing c, with

`c=\frac{(a-b)^2}4\implies\sqrt c=\frac2=\frac{b-a}2`

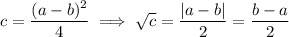
because
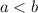`a<b`, gives

`I=\frac{b-a}2(\cos(2P)-\cos(2Q)-(P-Q))`

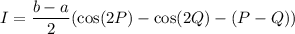
Without knowing p and q explicitly, there's not much more to say.