Question

Current research indicates that the distribution of the life expectancies of a certain protozoan is normal with a mean of 49 days and a standard deviation of 10.2 days. Find the probability that a simple random sample of 64 protozoa will have a mean life expectancy of 54 or more days.

Answer 1

The probability that a simple random sample of 64 protozoa will have a mean life expectancy of 54 or more days is P(M>54)=0.00004.

Explanation:

In this case, we have a population lifetime normally distributed with mean 49 and standard deviation 10.2.

We take a sample of size n=64.

Then, we can calculate the z-score for a sample mean M=54, in order to calculate P(M>54):

`z=(X-\mu)/(\sigma/√(n))=(54-49)/(10.2/√(64))=(5)/(1.275)=3.922\\\\\\P(M>54)=P(z>3.922)=0.00004`

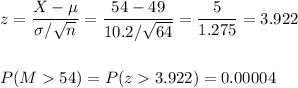
The probability that a simple random sample of 64 protozoa will have a mean life expectancy of 54 or more days is P(M>54)=0.00004.