Question

Let g be the function defined by g(x) = − 1 2 x + 5 if x < 6 x − 6 if x ≥ 6. Find g(−6), g(0), g(6), and g(12). g(−6) = g(0) = g(6) = g(12) =

Answer 1

g(-6) = 8; g(0) = 5; g(6) = 0; g(12) = 6

Explanation:

We assume your function definition is ...

`g(x)=\left\{\begin{array}{ccc}-(1)/(2)x+5&\text{for}&x<6\\x-6&\text{for}&x\ge 6\end{array}\right.`

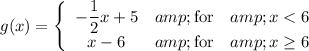
For each given value of x, determine which segment applies, then evaluate.

For x = -6 and for x = 0, the first segment applies:

g(-6) = (-1/2)(-6) +5 = 3 +5 = 8

g(0) = (-1/2)(0) +5 = 5

For x = 6 and x = 12, the second segment applies:

g(6) = (6) -6 = 0

g(12) = (12) -6 = 6

In summary, ...

g(-6) = 8; g(0) = 5; g(6) = 0; g(12) = 6